rechne.exe

rechne.exe is an open source command line calculator which is highly functional and easy to use. It supports a lot of mathematical functions, complex numbers, calculation with big numbers, calculation with geo coordinates and is well documented.

Download rechne.exe Version 3.1 • English • Windows (64 Bit) All files and versions

Features

provides an easy-to-use interactive shell mode
can easily be intergrated into shell scripts
can transfer numbers from any numbering system into any other (e.g.: binary numbers into hex numbers into decimal numbers...)
can handle complex numbers
provides over 60 mathematical functions, such as log, sin, cos, ...
provides detailled manual pages with many examples on how to use rechne.exe or a particular function
allows for unlimited nesting of terms by the use of brackets
allows for saving numbers under a name, e.g. for a frequent use
allows for referencing the last solutions in your current input
provides a big-number mode for calculation with very large integers (RSA 4096 is no problem)
provides a static/dynamic library for easy integration in other programs
allows for defining own functions
provides a geo mode for calculation with geo coordinates

Options

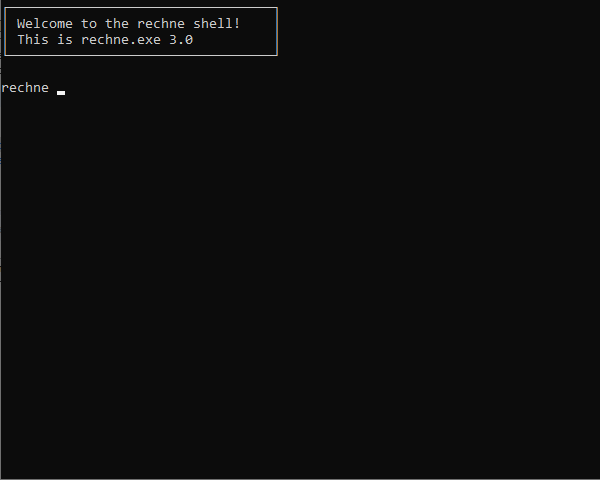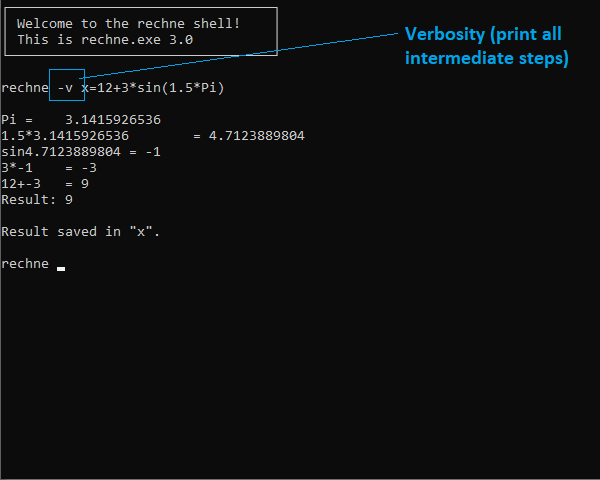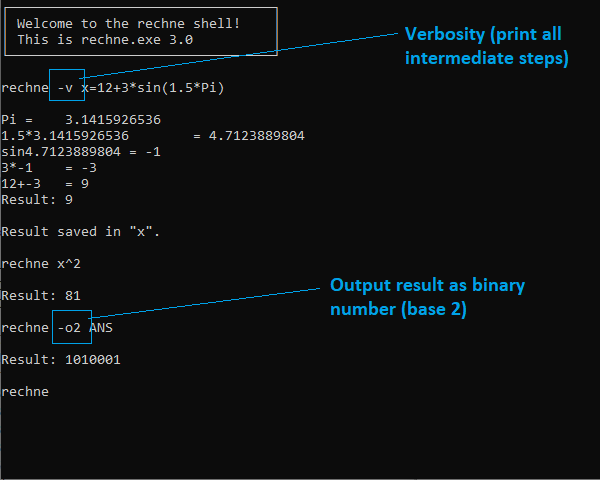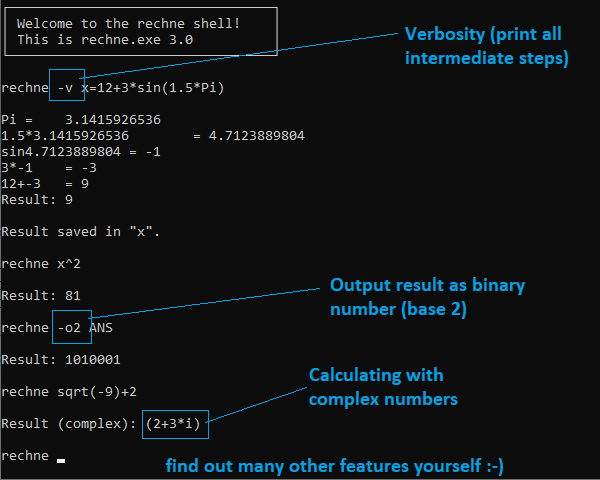
`-v`	Verbosity: print all intermediate steps. Example: `rechne -v 12+3sin(1.5Pi)`
`-q`	Quiet: only print the final result. Example: `rechne -q 12+3sin(1.5Pi)`
`-y`	Force: answer all questions with yes. Example: `rechne -y Pi=3.14`
`-p [x]`	Precision: print numbers with [x] decimal places. Default is scientific (as many places as needed). Example: `rechne -p5 Pi^2`
`-i [x]`	Input numeral system (default is 10 → decimal numbers). Example: input binary number: `rechne -i2 1101011100`
`-o [x]`	Output numeral system (default is 10 → decimal numbers). Example: output hexadecimal number: `rechne -o16 123456`
`-o polar`	Print complex numbers in polar format (default is arithmetic format). Example: `rechne -opolar sqrt(-4)+3`

The options can be combined.
Example: take binary numbers as input, output as hexadecimal numbers and print all intermediate steps:


rechne -i2 -o16 -v (11101-111)^10


11101 -> 29
111 -> 7
10 -> 2
29-7    = 22
22^2    = 484
484 -> 1E4
Result: 1E4

Supported functions/operations

modulus	mod	factorial	fac	raising	^
shift decimal point	E	root	rt	square root	sqrt
logarithm	log	natural logarithm	ln	decimal logarithm	lg
binary logarithm	ld	parallel operation	//	binominal coefficient	binom
sinc function	si	sine	sin	cosine	cos
tangent	tan	secant	sec	cosecant	csc
cotangent	cot	arcsine	asin	arccosine	acos
arctangent	atan	arcsecant	asec	arccosecant	acsc
arccotangent	acot	hyperbolic sine	sinh	hyperbolic cosine	cosh
hyperbolic tangent	tanh	hyperbolic cotangent	coth	area hyperbolic sine	asinh
area hyperbolic cosine	acosh	area hyperbolic tangent	atanh	area hyperbolic cotangent	acoth
numerical integral	sum	product integral	prd	definite integral	int
random number	rand	fibonacci sequence	fib	signum function	sig
round-down	floor	round-up	ceil	real part	creal
imaginary part	cimg	absolute value	cabs	polar angle	carg
greatest real number	max	smallest real number	min	greatest magnitude	maxc
smallest magnitude	minc	greatest common divisor	gcd	least common multiple	lcm
factorization	factor	digit sum	ds	iterative digit sum	dsi
digit product	dp	iterative digit product	dpi	previous results	ANS
Pi	Pi	Eulers number	e	imaginary unit	i

Manual pages provide more information about a certain function and how to use it.
Example: rechne sqrt ?

Big number mode

Of course the rechne.exe default mode supports calculating with big numbers. However from a certain size on some precision (least significant digits) gets lost. This is because the operating systems use floating point objects which by nature are limited.
But some application (e.g. cryptography) require exact results. In this sense "big numbers" are only a stream of bytes. This is what the big number mode is for.
Type rechne bn to enter the big number mode. By default all inputs are hexadecimal (upper case!). Not all functions/operations from the default mode are implemented here. Type help to see what functions/options are implemented.

Big number options

`-v`	Verbosity: print all intermediate steps and print a memory & time usage summary at the end. Example: `rechne@bn -v AFFE007\|FF`
`-p`	Plain output: do not format the output numbers. Example: `rechne@bn -p AFFE007`
`-q`	Quiet: only print the final result. Example: `rechne@bn -q AFFE007\|FF`
`-y`	Force: answer all questions with yes. Example: `rechne@bn -y rand(8000)`
`-s [file]`	Save the resulting big number to a file with name [file]. In contrast to normal assignments the file will still be there, after rechne.exe has exited. Written numbers can be read with the `read` function. PLEASE NOTE: writing the file uses the currently set output format (by default hex). This format has to be used as input format when reading again. Example: `rechne@bn -s myprime1 prime(100)rechne@bn read(myprime1)`
`-i [x]`	Input format where [x] can be one of `dec` → for decimal numbers `low` → for hexadecimal lower case `bin` → for binary numbers `b64` → for base64 code `x` → for machine code binary . Example: input decimal number: `rechne@bn -i dec 6432876431526887987`
`-o [x]`	Output format, same values for [x] possible as with -i. Example: output binary number: `rechne@bn -o bin AFFE007`
`-f/-l [x]`	Print the first or last [x] bytes of the big number only. Example: only print first 10 bytes of a large random number: `rechne@bn -f 10 rand(1000)`

Big number functions

`(a)mod(b)`	Modulo: the rest of the division of two numbers 'a/b'. Example: `rechne@bn AFFE007modABC`
`(a)pow(b)`	Exponentiation: raising 'a' to power 'b'. Example: `rechne@bn AFFE007pow2`
`(a)pow(b)mod(c)`	Exponentiation with Modulo: especially for use in RSA crypto. Example: `rechne@bn AFFE007pow2modABC`
`sqrt(a)`	Square root of input number 'a' (Herons algorithm). Example: `rechne@bn sqrt(AFFE007)`
`rand(a)`	Create a random number with 'a' bits. Example: `rechne@bn -idec rand(1024)`
`read(file)`	Read a previously (with -s) written number from a file.
`gcd(a,b)`	Greatest common divisor of two numbers 'a' and 'b'. Example: `rechne@bn gcd(AFFE00C,ABC)`
`mrt(a,b)`	Miller-Rabin-Test: returns 1 if 'a' is a (probable) prime number, tested with coefficient b. Example: `rechne@bn mrt(AFFE007,101)`
`prime(a)`	Find a prime number with 'a' bits. This will generate odd random numbers of size 'a' and apply the Miller-Rabin-Test. Example: `rechne@bn -idec prime(1024)`
`eea(a,b)`	Find the multiplicative inverse of 'a mod b' using the extended Euklidean algorithm. Example: `rechne@bn -idec eea(99,78)`

Sample snippets

Example 1: Convert a hexadecimal number to decimal:rechne@bn -o dec AFFE007
Example 2: Get a prime number of size 1024 bits and save to local variable 'p':rechne@bn p=prime(400) (why 400 and not 1024? Because ALL numbers are hexadecimal if not otherwise specified. So 1024(dec) = 400(hex) )
PLEASE NOTE: generating big prime numbers may take some while and can heat up the CPU quite a bit. Many random numbers of the requested size are created and checked for primality (using the Miller-Rabin-Test), which is costly.

Example 3: Read a JPEG file and print the first 10 bytes:rechne@bn -ix -f10 read(picture.jpg) ('-ix' tells the program to expect non-ASCII byte code)
PLEASE NOTE: the '-f/-l' option only affects the printing of the big numbers but has no effect on the internal representation. So in the background the entire file is read and held as a big number.

Example 4: Write a hex number to binary file:rechne@bn -ox AFFE007 > myfile ('-ox' tells the program to output non-ASCII byte code and '>' redirects all outputs to the file 'myfile')
Alternatively: rechne@bn -s myfile -ox AFFE007 ('-s' writes the result to the file named 'myfile' with the specified output format)

Example 5: Convert Base64 code to a hex number:rechne@bn -i b64 YW55IGNhcm5hbCBwbGVhc3VyZQ==Of course base64 can also be read from a file (using rechne@bn -i b64 read(file)). But often base64 file include a header like '-----BEGIN PGP MESSAGE-----' or similar. PLEASE NOTE: This header needs to be removed manually before reading so the file only contains the plain base64 code!

Example 6: Apply a bit mask and shift 4 bits to the left:rechne@bn (AFFE007&FFFF000)<<4
Example 7: Write hexadecimal letters from a human readable file as actual byte code:rechne@bn -ox read(hexfile.txt) > bytefile

Putting it together: a step by step RSA-2048 encryption

`rechne@bn -s prime_p -i dec var_p=prime(1024)`	Create a 1024 bit prime number (attention: this might take a while!) and save it to file 'prime_p'. This file remains after rechne.exe has exited so this process only has to be performed once. The assignment to local variable 'var_p' only exists while rechne.exe is running.
`rechne@bn -s prime_q -i dec var_q=prime(1024)`	Same with a second prime number → 'prime_q'.
`rechne@bn -idec pub_e=65537`	Define the public exponent 65537.
`rechne@bn n=var_p*var_q`	Calculate the modulus n=p*q.
`rechne@bn r=(var_p-1)*(var_q-1)`	Calculate r=(p-1)*(q-1).
`rechne@bn gcd(pub_e,r)`	Make sure the greatest common divisor of pub_e and r equals 1.
`rechne@bn priv_d=(eea(r,pub_e)+r)mod(r)`	Calculate the private exponent 'priv_d' using the extended Euklidean algorithm (eea). So 'priv_d' is the multiplicative inverse to 'pub_e modulo r'. The supplement '(...+r)mod(r)' is just to make sure 'priv_d' is always positive.
`rechne@bn plain_text=read(plain.txt)`	Read a plain text file and assign the conent to a local varibale. This example DOES NOT cover padding!
`rechne@bn -s encrypted (plain_text)pow(pub_e)mod(n)`	Perform the encryption and write the result to a file named 'encrypted'. This example DOES NOT cover padding!
`rechne@bn -s decrypted (read(encrpyted))pow(priv_d)mod(n)`	Perform the decryption and write the result to a file named 'decrypted'. This will only work if e*d=1 (mod r).
`rechne@bn read(decrypted)==plain_text`	Compare the decrypted number with the plain_text number. 1 (true) means both are equal.

Geo mode

In geo mode rechne.exe can process geo coordinates, convert them and perform some calculations.
Type rechne geo to enter the geo mode. Type help for more information.

The input of geo coordinates can have two diffrent formats:

Latitude,Longitude format: 51.339508,12.381132
Decimal minutes format: N51°20.370,E012°22.868

PLEASE NOTE: make sure there are no spaces in the coordinates. Latitude and longitude must be separated by a comma.

For calculations such as bearing and distance measuring rechne.exe is using Vincentys formulae which is a bit more precise than Haversine, considering Earths spherical anomaly.

When a coordinate is entered and successfully parsed by rechne.exe the output contains conversions into different coordinate formats and some basic geographical information. A geo coordinate is called a 'point'.
Example:


rechne@geo 51.339508,12.381132


                        51.339508,12.381132
    in decimal minutes: N51°20.370,E012°22.868
    in minutes&seconds: N51°20'22.2",E012°22'52.1"
                   UTM: 33U E317593 N5690837
    openstreetmap link: https://www.openstreetmap.org/?mlat=51.339508&mlon=12.381132#map=16/51.339508/12.381132

Distance -> to Prime meridian:      861743 m
         -> to Equator:            5689857 m
         -> to North pole:         4312109 m
         -> to South pole:        15691822 m
--------------------------------------------------

Points can be assigned a variable name to store them during this session: rechne@geo berlin=52.516250,13.377711

Two points stored

As soon as multiple points are stored, the program outputs information on the difference of both points:


rechne@geo leipzig=51.339508,12.381132


leipzig               : 51.339508,12.381132
    in decimal minutes: N51°20.370,E012°22.868
    in minutes&seconds: N51°20'22.2",E012°22'52.1"
                   UTM: 33U E317593 N5690837
    openstreetmap link: https://www.openstreetmap.org/?mlat=51.339508&mlon=12.381132#map=16/51.339508/12.381132

Distance -> to Prime meridian:      861743 m
         -> to Equator:            5689857 m
         -> to North pole:         4312109 m
         -> to South pole:        15691822 m
         -> to berlin:              147789 m

Azimuth (median):
         leipzig->berlin:  27.6°         berlin->leipzig: 207.6°

Midpoint:
         leipzig-><-berlin: 51.926854,12.879421

North-South difference:
         leipzig<-->berlin:     130931 m

East-West difference:
         leipzig<-->berlin:      67652 m
--------------------------------------------------

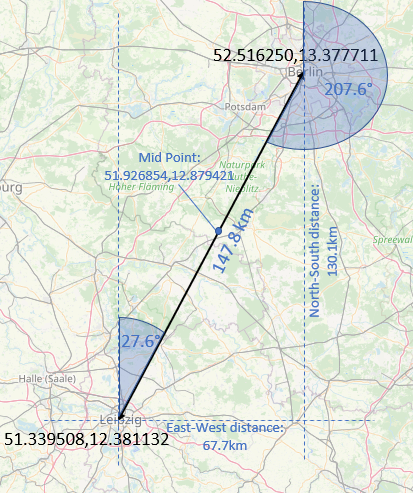The printed information contains:

distance between both points
azimuth between both points
coordinates of the mid point
North-South distance
East-West distance

Please note: azimuths don't always sum up to 360°. This is because geometry on a spherical is a bit different than on a plane area.

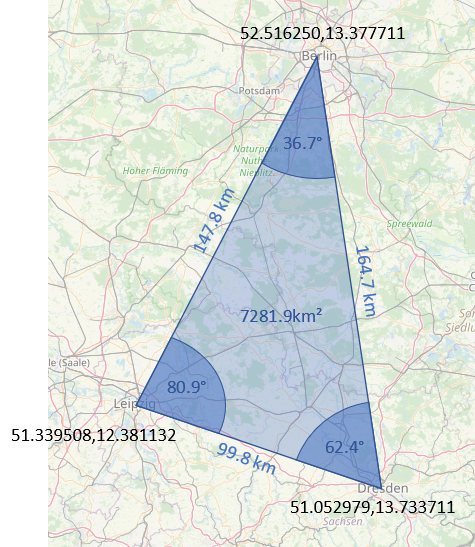
Three points stored

As soon as a third point is stored, the program calculates the area of the resulting triangle and the enclosed azimuths.


rechne@geo dresden=51.052979,13.733711


dresden               : 51.052979,13.733711
    in decimal minutes: N51°3.179,E013°44.023
    in minutes&seconds: N51°3'10.7",E013°44'1.4"
                   UTM: 33U E411248 N5656479
    openstreetmap link: https://www.openstreetmap.org/?mlat=51.052...

Distance -> to Prime meridian:      961579 m
         -> to Equator:            5657980 m
         -> to North pole:         4343986 m
         -> to South pole:        15659945 m
         -> to berlin:              164651 m
         -> to leipzig:              99774 m

Azimuth (median):
         dresden->berlin: 351.4°         berlin->dresden: 171.4°
         dresden->leipzig: 288.6°         leipzig->dresden: 108.6°

Midpoint:
         dresden-><-berlin: 51.784526,13.555711
         dresden-><-leipzig: 51.194291,13.057422

North-South difference:
         dresden<-->berlin:     162808 m
         dresden<-->leipzig:      31877 m

East-West difference:
         dresden<-->berlin:      24167 m
         dresden<-->leipzig:      94252 m

Triangle dresden,berlin,leipzig:
         enclosed angle dresden:  62.4°
         enclosed angle berlin:  36.7°
         enclosed angle leipzig:  80.9°
         surface area: 7281.9 km²
--------------------------------------------------

Remove all points

Adding four or more points increases the output lines heavily because from each new point all distances, azimuths and triangles are calculated to all existing points.
With rechne@geo clear all stored points/lines are removed.

Apply a bearing

With the syntax [src]->[distance],[azimuth] the point donoted by [src] can be moved by the specified distance and azimuth which results in a new point.
[src] can either be direct coordinates or the name of a previously stored point.

Example 1: rechne@geo 51.052979,13.733711->123m,117° is creating a point which is 123m and 117 degrees from the coordinates.
Example 2: rechne@geo berlin->1.5km,1.711 is creating a point which is 1500m and 98 degrees (=1.711 RAD) from the point with name 'berlin'.
Example 3: rechne@geo hamburg=berlin->298°,255km is creating and storing a point named 'hamburg' which is 255km and 298 degrees from the point named 'berlin'.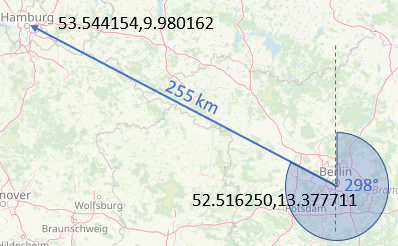

Draw a line between two points

With the option -d [src] [dst] a geographical line between point [src] and [dst] is drawn. The two points can be donoted directly by coordinates or by the name of previously stored points.
The output is basically the same as if entering the points directly. However lines can only be created using the '-d' option. The name of the line is hard-coded 'line' followed by an index.

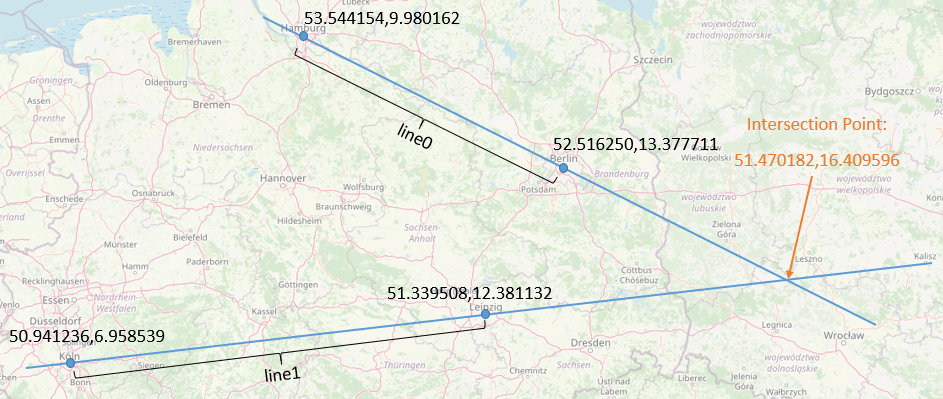
Example 1: draw a line named 'line0' between the previously stored points 'hamburg' and 'berlin'.


rechne@geo -d hamburg berlin


from 53.544154,9.980162 to 52.516250,13.377711:
                     Distance:     255000 m
            Azimuth (initial):     115.29 °
              Azimuth (final):     118.00 °
             Azimuth (median):     116.64 °

line 'line0' added

Example 2: draw a line named 'line1' between two direct coordinates; the first in latitude,longitude format; the second in decimal minutes format.


rechne@geo -d 50.941236,6.958539 N51°20.370,E012°22.868


from 50.941236,6.958539 to 51.339500,12.381133:
                     Distance:     381992 m
            Azimuth (initial):      81.23 °
              Azimuth (final):      85.46 °
             Azimuth (median):      83.35 °

line 'line1' added

Intersection of two geographical lines

Continuing from the previous section the existance of geographical lines can be used to calculate the intersection point between two lines. The function to use is cut(line0,line1) where 'line0' and 'line1' are the names of the previously stored lines (using the '-d' option).


rechne@geo cut(line0,line1)


                        51.470182,16.409596
    in decimal minutes: N51°28.211,E016°24.576
    in minutes&seconds: N51°28'12.7",E016°24'34.5"
                   UTM: 33U E597906 N5703055
    openstreetmap link: https://www.openstreetmap.org/?mlat=51.470182&mlon=16.409596#map=16/51.470182/16.409596

Distance -> to Prime meridian:     1137843 m
         -> to Equator:            5704395 m
         -> to North pole:         4297571 m
         -> to South pole:        15706361 m
         -> to berlin:              238546 m
         -> to hamburg:             493546 m
		 
...

License

rechne.exe and its sources are published under the GNU General Public License (version 3). Feel free to use, copy or edit rechne.exe under the terms of this license.
Please note: As stated in GPL rechne.exe comes with absolutely no warranty.
A copy of this license comes with the download archive.